Existence and boundary behaviour of positive solutions for a coupled fractional system Online publication date: Fri, 02-Sep-2022
by Imen Ben Saad; Sameh Turki; Zagharide Zine El Abidine
International Journal of Dynamical Systems and Differential Equations (IJDSDE), Vol. 12, No. 3, 2022
Abstract: We consider the following semilinear fractional system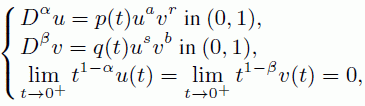
where α, β ∈ (0,1), a, b ∈ (-1, 1), r, s ∈ ℝ such that (1 -|a|)(1 - |b|) - |rs| > 0,Dα,Dβ are the Riemann-Liouville fractional derivatives of orders α, β and the nonlinearities p, q are positive measurable functions on (0, 1). Applying the Schäuder fixed point theorem, we establish the existence and the boundary behaviour of positive solutions in the space of weighted continuous functions.
Existing subscribers:
Go to Inderscience Online Journals to access the Full Text of this article.
If you are not a subscriber and you just want to read the full contents of this article, buy online access here.Complimentary Subscribers, Editors or Members of the Editorial Board of the International Journal of Dynamical Systems and Differential Equations (IJDSDE):
Login with your Inderscience username and password:
Want to subscribe?
A subscription gives you complete access to all articles in the current issue, as well as to all articles in the previous three years (where applicable). See our Orders page to subscribe.
If you still need assistance, please email subs@inderscience.com